刘 徽
从公元220年东汉分裂，到581年隋朝建立，史称魏晋南北朝。这是中国历史上的动荡时期，但同时也是思想相对活跃的时期。在长期的独尊儒学之后，学术界思辨之风逐渐兴起。在数学上也有了论证的趋势，其表现是对《周髀算经》、《九章算术》等经典数学书籍的注释。这方面的杰出代表是刘徽和祖冲之父子。
对刘徽的生卒时间，史学界尚无确认。据《隋书》记载，刘徽于公元263年撰写了《九章算术注》，这部著作奠定了他在中国数学史上的不朽地位。刘徽数学成就中，最突出的是“割圆术”和体积立论。
1.割圆术
在《九章算术》方田章“圆田术”注中，刘徽提出了“割圆术”，并以此方法作为计算圆的周长、面积和圆周率的基础。“割圆术”的主要思想是利用圆的内接正多边形去逐步逼近圆。他本人对这种方法的解释是“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”
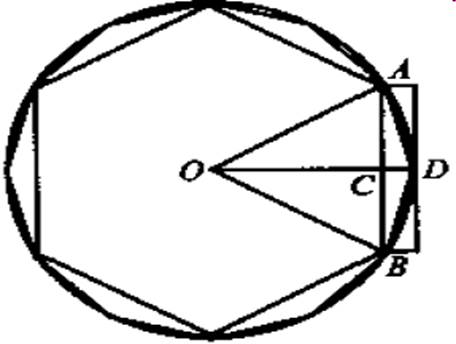
割圆术
刘徽从圆的内接正六边形出发，并取半径为1尺，将边数逐次加倍，并计算逐次得到的正多边形的周长和面积。他一直计算到了192边形，得出了圆周率的精确到小数后二位的近似值
，对应的分数是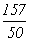
，这就是有名的“徽率”。刘徽同时指出，将“割圆术”继续下去，可以得出更精密的圆周率的近似值。
刘徽是中国数学史上第一位建立可靠理论推导、计算圆周率及其近似值的数学家。
2.体积理论
刘徽对面积与体积公式的推证，取得了超越时代的成果。
刘徽对面积与体积的推证，建立在他所谓的“出入相补”原理：一个几何图形（平面的或立体的）被分割成若干个部分后，面积或体积的总和保持不变。
利用这条原理，刘徽成功地证明了《九章算术》中的很多面积公式，但转向推证立体的体积公式时，却遇到了困难。像一些一流的数学家一样，他灵活地采用了无限小方法：极限方法和不可分量方法，从而成功地得到了很多体积公式。
在对球体积公式的推证过程中，刘徽做出了重要贡献。他首先指出，《九章算术》中所给出的球的体积公式是不正确的。刘徽创造了一个新的立体图形“牟合方盖”：在一立方体内作两个相互垂直的内切圆柱，这两个圆柱体相交的的部分即是牟合方盖。并指出，只要算出牟合方盖的体积，球的体积也就唾手可得。重要的是，刘徽得到了球的体积与牟合方盖的体积之比等于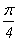
。但他最终没能找到计算牟合方盖体积的方法。
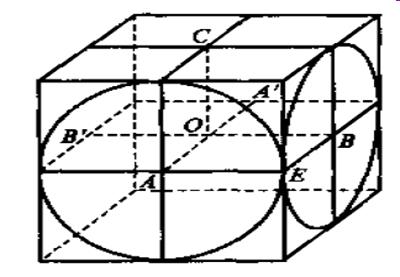
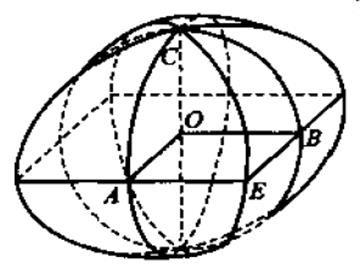
牟合方盖
刘徽虽未能求出球的体积公式，但他提出的不可分量方法和牟合方盖影响甚大。后来祖冲之父子正是采用刘徽的这种方法，推证出了正确的球体积公式。
