高斯(1777-1855)出生于德国Brünswick一穷困人家。他从小就算学异禀。他的才智受到当地Brünswick公爵的关注,公爵就一直资助他完成大学教育,取得博士学位,并出版数学巨著《整数论研考》。
高斯年冠十九,就在数学上有登峰造极的表现:他突破数学史上两千多年的沉寂,以直尺与圆规作出正十七边形的图形来。而且他维持如此杰出的研究质量达半个世纪之久。他的研究范围广泛,遍及纯数学与应用数学,研究内容新颖、深入。这使他成为十九世纪科学领域上最突出的人物。他在曲面学上的研究,更是导引黎曼创造黎曼几何学,并诱发二十世纪初爱因斯坦作出一般相对论。
一、身世
高斯的祖先姓 Goos,是德国北部 Vlkenrod村的新教徒人家。高斯的祖父 Jürgen Goos 是曾祖父Heinrich Goos三次婚姻中最后第二个儿子,在家他没有什么份量,只能往外地求发展。他结婚后于1739 年到Brünswick-Wolfenbüttel公国的首都Brünswick定居,改姓Gauss。起先由于没有置产,在当时的同业工会的限制下,只能做零工糊口。好不容易贷款购得一所小房子居住了十四年,生育三男一女。后来换房子到Wilhelm街30号。1774年7月5日债未还清,他就因肺病去世。他的妻子早他三个月故去。长子Gebhard一向帮助他父亲做工,就由他负责偿债。不过他也跟弟妹谈好,房子归他继承,弟妹分得一些现款(借来的)做为补偿。这些债Gebhard费了二十五年才还清。
Gebhard在1768年与Dorothea Vernecke结婚,第二年1月14日生子Johann Georg Heinrich。1775年9月5日他的妻子因肺病去世。1776年4月25日 Gebhard与邻村的Dorothea Bentz再婚。1777年4月30日他们在 Wilhelm 街30号的家里生下数学天才高斯.高斯是 Dorothea 唯一的孩子。Dorothea在结婚前当过7年女佣。她没有正式受过教育,不会书写,印刷体字勉强可以念。
Gebhard做过各式各样的工作,最后十五年他只从事造园业。由于他会书写,也会计算,他当过一家葬仪社的会计。
高斯曾经向他的再婚对象Minna Waldeck描述过他父母亲:“父亲是一位老实、忠厚的人,在外头他得别人的尊敬。但是在家里他是个暴君。好在我很早就不用依靠他,彼此间的冲突较少。母亲个性坚强、明朗、善良又聪明。在我与父亲有冲突的时候,她很袒护我。我很敬爱她。”
二、幼少年时代
高斯7岁时进St. Cathrine小学。老师是J.B.Büttner。班上有百来个学生。老师在屋顶低、地板凹凸不平的教室里拿着鞭子来回走动。 鞭子是老师教、惩两用的。高斯在这样的环境下平安无事过了两年。在高斯九岁左右时,Büttner在算术课上要学生们“写出1到100的数字来,并求出它们的总和”。写好的同学把运算用的石盘(当时纸张还是奢侈品)翻下放在老师桌子上。再来交的同学依次叠上石板。老师想,出这样的考题他可以清静一下了吧。没想到高斯一下子就把石盘拿去放在老师桌子上,说:“我交了。”其他小朋友汗流夹背地忙着运算。高斯静坐着,不理会老师奇怪的眼神。结果大部分的小朋友都错了,因而挨了打。高斯的石盘只见 5050 这个数字。他给老师的解释是:1 + 100 = 101,2 + 99 = 101,… ,50 + 51 = 101。所以 1 + 100等于有50对101,答案便是5050。
这件事的发生有它象征性的意义,终其一生高斯做出来的结果都是简洁而正确的。
三、大学时代
高斯在1795年10月5日注册,成为哥廷根大学数学系学生,这时候他拥有年金158 thaler与伙食费。他对将来的出路感到彷徨。语文与数学都是他喜爱的,而学语文以后出路较好。
在大学第一年他借的书有25本。其中20本是文科的书,只有5本是数学书。
1796年3月30日是高斯生涯中决定性的一天。从这一天起,他开始写那出名的科学日记。他把他的发现依次记载到1814年7月9日[日记在1898年从高斯在德国唯一 (也是唯一他见过)的孙子Carl August在Hamlin的家中找出]。3月30日的日记用拉丁文写着:“等分圆周的原理以及用几何方法十七等分圆分等等。
据说从这一天开始他决定从事数学的研究,而语文成为他终生喜爱学习的一个嗜好。
四、《整数论研考》的问世
1798年9月底回到Brünswick后,高斯前途未卜。但他不再回父母亲家而租屋在Wenden街。他写信给Bolyai,期盼公爵能在经济上继续支持他到找到工作为止。他也找过工作,但都失去机会。
当年10月他到赫尔姆施泰特大学,使用那里的图书。馆长善待他,数学教授J. F. Pfa(1765-1825)也对他很友好。他在忙着完成《Disguisitiones Arithmeticae》(编注:整数论研考,也译作算术研究)这本书。11月时他已订正第五章四次,第七章基本上完成了,第八章还得花好多时间。12月中旬公爵答应继续给高斯年金158 thaler。 在这以前年金迟迟未发下,高斯以借贷度日。公爵没有立即允诺继续给高斯年金有他个人的理由:他的父亲挥霍过度,使国库干枯,几近破产。公爵想了法子,才挽救了这个局面。
公爵要求高斯拿博士学位。高斯本来打算交给赫尔姆施泰特大学《Disqusitiones Arithmeticae》做为博士论文,但是印刷情况缓慢,高斯写的份量又越来越多,印刷费可观,超出预算。因此,高斯打住出版第八章的念头。在1799年4月高斯打算另交博士论文,选题为“代数学的基本定理”。5月他完成它交给赫尔姆施泰特大学当局。这是高斯做的有关“代数学的基本定理”第一次证明。此后他又用另一些方式给了它三次证明。
五、高斯的数学成就
这时候他开始展现大学时代天文学教授Seyer给他培养出来的兴趣:天文学。4月间他做出计算视差的公式来。他也研究算术几何平均数(arithmetico-geometric mean)、双纽线(lemniscate)与三角函数间的关系。
1808到1809年间,舒马赫(H. C. Schumacher,1780-1850)来哥廷根跟高斯学天文学。他记下他与高斯的对话成书,叫做《Gaussiana》。这本书对后世研究他们两人很有帮助。他们的交往持续到舒马赫去世。两人的书简集共六册。
高斯的第二部巨著《在太阳周围回转成圆锥曲线的天体之运动论》(Theoria motus corporum coelestium in sectionibus onicis Solem ambientium)在1809年成书,由当时最著名的出版商F. C. Pertes印刷。本来他用德文写,后来听从Pertes的意见,为普及起见写成拉丁文内容是高斯依据开普勒的法则,作出圆锥曲线(椭圆与双曲线;物线不适用)运动之下的天体轨道计算方法的完全体系。并从观测天体的三个点决定恒星或彗星轨道的一般方法。书的内容终于最小二乘法的解说。这本书以形式上简洁,文笔优雅、有完美性及独创性著称。当时常有新星出现,天文学家们不得不借它来计算星座的轨道,因此出版后有四十年之久它成为天文学家们必须精通的教科书。所以学者们对《运动论》的评价很高,世界各地的学会也就争聘高斯为他们的会员了。法国科学院更在1810年赠送他Lalande奖[为纪念法国数学家及天文学家J. J. Le Franc ais de Lalande(1732-1807)所设立的奖],高斯拒受。后来科学院秘书与Sophie Germain(1776-1831)动用奖金的一部分买一座天文摆钟送他,他这才接受,还终生摆设那一座钟在他的房间里。
1811年8月,天空上突然出现一颗闪亮的大彗星。高斯在8月22日黄昏时分看到它。几天后他开始观测,这时von Zach八月初旬的观测结果已经到手了。由这些高斯算出这颗大彗星的物线轨道。它再现时果然在高斯算出的轨道上,并印证他的预言,亮度增强了。而欧洲的人们则视这颗大彗星为一代霸主拿破仑开始落败的预兆。
1812年1月30日高斯在哥廷根皇家科学学会上发表超几何级数+1
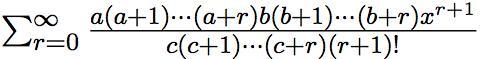
的论文。这个级数因a,b,c取特别的数而可成为二项级数、对数、三角函数等解析学上很重要的级数。高斯是首位对无限级数的收敛性做出研究的数学家。
1812年6月底拿破仑率领近45万大军攻打俄罗斯而取道德国。之前拉普拉斯向拿破仑进言请他对哥廷根大学特别关照。因为那儿住着当代最顶尖的数学家高斯。此后十年是高斯成果丰硕的时期。他出了二十数篇范围广泛的论文。其中有理论及观测天文学、曲面论、整数论及对数的问题等,还给代数基本定理另两种证明。