从物不知数问题到中国剩余定理
原创 Prime ideal 素理想 2020-08-12
从物不知数问题到中国剩余定理
物不知数问题是我国古代数学名著《孙子算经》中的一道非常有趣的题目:今有物不知其数,三三数之余二,五五数之余三,七七数之余二,问物几何?
如何解决像这样的一类问题呢?我们要从数的整除性入手,首先我们来介绍几个相关的概念.
整除
这里我们只在整数的范围类讨论整除的概念.
整除:设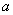 ,
,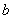 都是整数,若存在
都是整数,若存在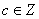 ,使得
,使得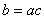 ,则称
,则称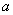 整除
整除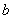 或
或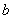 能被
能被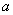 整除,记为
整除,记为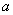
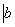 .
.
模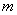 同余:设
同余:设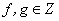 ,若
,若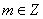 满足
满足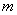
 ,则称
,则称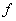 和
和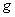 模
模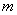 同余,记为
同余,记为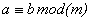 .
.
最大公因数:设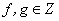 ,若
,若 满足
满足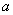
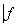 ,
,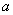
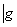 ,则称
,则称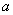 是
是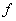 和
和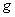 的公因数;若
的公因数;若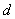 是
是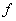 和
和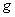 的一个公因数,并满足
的一个公因数,并满足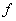 和
和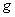 的任一个公因数都能整除
的任一个公因数都能整除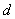 ,则称
,则称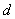 是
是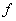 和
和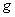 的最大公因数,记为
的最大公因数,记为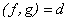 .
.
互素:若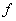 和
和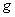 的最大公因数为1,则称
的最大公因数为1,则称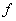 和
和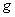 互素.
互素.
关于最大公因数,我们有如下定理:
定理1 若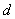 是
是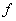 和
和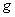 的最大公因数,则存在
的最大公因数,则存在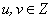 ,使得
,使得
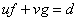 .
.
这一定理的证明需要用到辗转相除法,读者可以翻看参考文献1的P17,这里略去.
最后,我们在介绍一个关于互素的结论:
定理2 设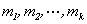 是两两互素的整数,则对
是两两互素的整数,则对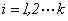 有
有
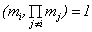 .
.
在有了这些预备的概念和结论后,我们就可来着手解决物不知数问题了.
物不知数问题的解法
我们设总数为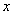 ,则由
,则由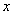 满足“三三数之余二,五五数之余三,七七数之余二”,可知
满足“三三数之余二,五五数之余三,七七数之余二”,可知
3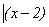 ,
,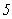
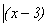 ,
,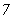
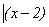
用同余的观点来看,也就是
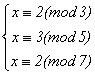
注意到是两两互素的,于是由定理2,我们有
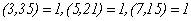
再由定理1,知存在 ,使得
,使得
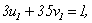
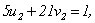
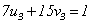
则
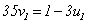 能被5和7整除,但被3除余1;
能被5和7整除,但被3除余1;
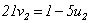 能被3和7整除,但被5除余1;
能被3和7整除,但被5除余1;
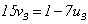 能被3和5整除,但被7除余1;
能被3和5整除,但被7除余1;
进一步得到
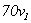 能被5和7整除,但被3除余2;
能被5和7整除,但被3除余2;
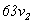 能被3和7整除,但被5除余3;
能被3和7整除,但被5除余3;
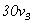 能被3和5整除,但被7除余2;
能被3和5整除,但被7除余2;
所以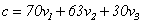 就是满足问题条件的一个解,而将
就是满足问题条件的一个解,而将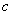 再加上3,5,7的倍数后所得到结果依然满足条件,于是该问题的通解就为
再加上3,5,7的倍数后所得到结果依然满足条件,于是该问题的通解就为
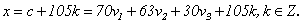
接下来,只要将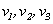 求出来便完全解决了这个问题.不难发现
求出来便完全解决了这个问题.不难发现
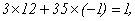
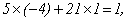
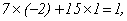
所以
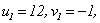

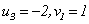
于是
 =23
=23
故原问题的通解就为
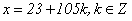 .
.
明朝数学家程大位在他的《算法统宗》中将求解物不知数问题的解答总结为一首歌诀:
三人同行七十稀,五树梅花廿一枝.
七子团圆正半月,除百零五便得知.
我们将上面求解物不知数问题的方法加以一般化,便可以得到著名的中国剩余定理
中国剩余定理设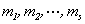 是两两互素的大于1的整数,则对于任意给定的整数
是两两互素的大于1的整数,则对于任意给定的整数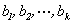 ,一次同余方程组
,一次同余方程组
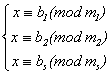
在Z中有解,并且它的通解为
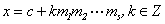
这里
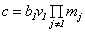 +
+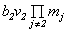 +...
+...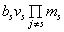
且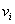 满足
满足
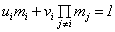
我们将上面分析物不知数问题的过程一般化便可以得到中国剩余定理的证明.
南宋数学家秦九韶在《数书九章》中系统的介绍了求解一次同余方程组的一般方法,秦九韶将他求解的方法称为"大衍求一术",本质上就是在做辗转相除法.秦九韶的方法是正确的但却没有给出证明,直至18,19世纪,Euler和Gauss分别对一次同余方程组做了研究,并独立地获得与秦九韶的"大衍求一术"相同的定理.年德国数学家Mattiessen首先指出秦九韶的方法和Gauss的算法是一致的,因此求解一次同余方程组的剩余定理被称为中国剩余定理.
韩信点兵问题
相信大家也一定听说过韩信点兵问题:
有一队士兵,五五数之余一,六六数之于五,七七数之余四,十一十一数之余十,问这一队士兵有多少人?
这个问题就是物不知数问题,请读者利用中国剩余定理去解决它.
参考文献
1.数学的思维方式与创新,丘维声,北京大学出版社 2.数学文化,顾沛,高等教育出版社